António S. Pinto Barbosa, Professor of Economics at the New University of Lisbon, former student of Jim, with doctoral thesis written under his supervision, and co-author.
The constitutional stage revisited
1
In a short article written in 1964 in celebration of the sixtieth birthday of Professor A.P. Lerner, Paul Samuelson criticized the notion of the ‘veil of ignorance’ used in the Economics of Control.
2 Lerner (1944) advanced such concept to derive the strong proposition according to which in society"the ... probable value of total satisfactions is maximized by dividing income evenly."
Samuelson's point of contention, however, was not directed at the egalitarian result as such but at the use of the very notion of equal ignorance from which it was ultimately derived. Specifically, he argued:
"If I have a beautiful singing voice, a pretty face, a high I.Q., an inherited title, or the gift of salesmanship, I shall be stupid to think that the egalitarian state is the safest hedged state for me. I don't expect the inegalitarian state to deal me a random selection of the cards. My ignorance is balanced around a favourable deal and I shall certainly not make the vote unanimous even if I have concave utility."(p. 176)
This quotation raises an important question in the area of constitutional economics. In fact, one can ask: What kind of motivation might persuade a rational individual, who happens to know, here and today, his own specific position in the social setting, to admit embarking on the choice of income distribution under the veil of ignorance? That is, even if we abstract from such complications as how to operationally generate the ‘veil of ignorance’, some rationale seems to be required to justify a preference for such choice-setting in the first place.
Amidst many other outstanding contributions to the foundation and development of constitutional economics, I think we owe, here again, to Jim Buchanan a decisive contribution to the clarification of such central question. As I have been, at some earlier point, similarly interested and intrigued by Samuelson's objection to the notion of the veil of ignorance, I thought that Jim's 80 birthday would be an excellent occasion to briefly revisit such topic.
For that purpose I take a most simple description of a constitutional decision on the division of social income under the veil of ignorance. I assume two individuals, A and B, who have to choose how to allocate a fixed social income, Y, normalized for convenience to unity, between two positions, according to shares
q and 1-q , (0<q <1). For simplicity, suppose that both individuals possess a same strictly concave utility function of income, U(Yi), i = A,B. Consider now the viewpoint of one of these individuals, say A, under a generalized notion of the veil of ignorance. Specifically, assume that A has to choose optimal q so as to maximize his expected utility as given by(1) S(p
1,p2,q ) = p1U(q ) + p2U(1-q ),where p
1 and p2= 1 - p1 indicate de probability A subjectively assigns to the occupation of the two alternative positions. Under complete ignorance (the ‘equal ignorance’ case analysed by Lerner and Samuelson) it would be appropriate to assume an equal probability of occupation of the two possible positions:(2) p
1 = p2 = 1/2.However, expression (2) might simply represent a limiting case of a generalized notion of the veil of ignorance. In fact, one can envisage a continuum of situations where, at one extreme, A knows with certainty his social position, say, the position he currently holds, p
1=1, p2 = 03. Under Samuelson's terminology he knows whether he possesses a beautiful singing voice, a pretty face or a high I.Q. From this extreme, as uncertainty increases, one can assume that p1 declines monotonically (p2 increases) until the ‘equal ignorance’ limiting situation (2) is eventually attained. Suppose, therefore, that this variable degree of uncertainty is represented by t , so that p1= p1(t ), p2= p2(t ) and(3) p
1(0) = 1, dp1/dt < 0, lim t® M p1(t ) = 1/2,where M corresponds to some limiting situation of complete uncertainty in which Lerner's ‘equal ignorance’ prevails. One possible descriptive interpretation of the index t is the following: it might represent the time interval between some initial moment where, under the veil of ignorance, A chooses
q (the constitutional stage) and a subsequent moment where, under individual knowledge of the specific social positions occupied, a lagged implementation of that distributive choice takes place.4Taking a given degree of uncertainty, i.e. a specific value for t, under this generalized notion of the veil of ignorance, there is some optimal
q from the standpoint of A, call it q *(t ).5 Except for the limiting case of an equal probability of occupation, B would most likely find a different value for his optimal q . To obtain a collective decision, some bargaining and possibly some compromise between A and B seems, therefore, required.Under the most favorable circumstances for A, in which his optimal solution would prevail as the constitutional colective choice, the corresponding expected value for A may be represented by
(5) S*(t ) = S[p
1(t ),p2(t ),q *(t )].As indicated, this value is dependent on the degree of uncertainty, t, which was assumed exogeneously given.
Now, it can be shown that S* declines uniformly as the degree of uncertainty increases, thus indicating that, from the standpoint of A, the amount obtainable under the most favorable circumstances diminishes. From his standpoint the game seems to become, so to speak, increasingly uninteresting. This is perhaps not too surprising a result in view of the fact that the veil of ignorance contributes to a sort of depersonalization, rendering A in the limit formally indistinguishable from B. In view of the antecipated decline on expected utility, one may therefore ask what kind of motivation might induce A, if he has to choose t , to prefer a choice setting involving increased uncertainty? In other words, since one would not expect the inegalitarian state, as Samuelson puts it, ‘to deal ... a random selection of the cards’, what kind of logic might favour such solution?
To rationalize the potential emergence of individual interest in the use of the veil of ignorance as a decision-making framework some element seems, therefore, to be missing in the foregoing analysis. This critical element has, in my interpretation, been advanced by Jim Buchanan when he demonstrated the central role played by decision-making costs savings as a result of increased uncertainty.
6 These bargaining costs savings, in turn, stem from the fact that the veil of ignorance tends to render the separate individual choices at the constitutional stage more similar to each other."The inherent uncertainty in choice among rules makes consensus among separate players much more likely to be attained than might otherwise be expected" (Buchanan, (1967), p.218.)
The individuals become more agreeable and unanimity may even be attained in the limiting situation of ‘equal ignorance’. In other words, the above analysis is, so far, incomplete since it does not take into account the absortion of resources associated with decision-making. To allow for this factor suppose decision-making costs, C, take the following simple form:
(6) C(t) = c
b -t , 0 £ t <M,= c
b -M, t ³ M.where
b >1 and 0<c<1. We thus assume that decision-making costs decline as uncertainty increases. When there is no uncertainty, (t =0), decision-making costs attain a maximum fraction of total social income, c (0<c<1). As the degree of uncertainty associated to the occupation of social positions increases, C declines (monotonically) approaching a minimum value under ‘equal ignorance’ (t ³ M). With this specification, the net amount of social income available fordistribution is(7) 1 - c
b -t.Assuming that the distributive shares
q and 1-q , to be constitutionally chosen, apply to this net income, the expected utility A obtains, given t , is now modified to7(8) S(p
1,p2,q ) = p1U[q (1 - cb -t)] +p2U[(1-q )(1 - cb -t)]Let
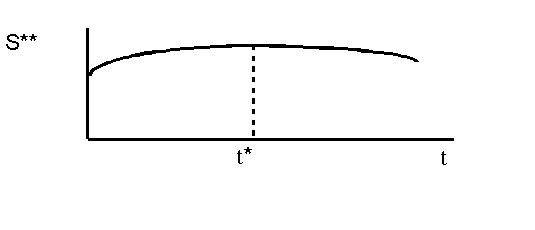
q ** indicate A's optimal choice of q under these circumstances and let S** indicate the corresponding expected value he obtains when such choice prevails. It is now possible, though by no means certain, that this expected value might increase with t. This suggests that the prospect of solving the distributive question through constitutional means is, in such case, well grounded in individual motivation. The random selection of cards, to use Samuelson's words, seems to be in accordance to individual interest. If the costs of decision-making are significant (c large) and decline rapidly with increased uncertainty (b large) that possibility might happen, as illustrated in the diagram below, where S** is plotted against the degree of uncertainty at the constitutional stage.
Figure 1: Expected value of A's most-preferred choice.
The diagram also indicates the value t* corresponding to the maximum expected value for the constitutional prospect. Under the interpretation suggested above for t, t* might represent the optimal lag, from A's standpoint, between decision and implementation of the distributive choice.
We might conclude by stressing again that some element seems to be often missing in the analysis of the individual choice calculus at the constitutional stage. This analysis typically highlights the redistributive ethical properties potentially associated with decisions taken in that framework. However, when the adoption of such framework is to be based on efficiency grounds, it is necessary to justify how optimizing individuals might find in their own interest to choose under a veil of ignorance. This motivational element seems needed the more so since the expected value of individual most-preferred choices declines with increased uncertainty under the veil of ignorance. The critical missing element is the decision-making costs savings obtainable at the constitutional stage. The recognition of its central role represents, in my view, one of the fundamental contributions Jim Buchanan brought to the area of Constitutional Economics.
Notes
1) I would like to thank the comments on an earlier version received from Vasco Santos, Mario Pascoa, Paulo Barcia, Duarte Brito and Pedro P. Barros.
2) The term ‘veil of ignorance’ was due, of course, to Rawls (1972)
3) A symmetric reasoning is assumed for B.
4) I ignore here discounting. I recall at this point the particular instance of lagged implementation of the Rignano tax plan in Italy suggested by Jim Buchanan (1967, p.299). Elsewhere (Barbosa, 1978) I have used the term vacatio legis to describe this same time interval.
5) Under this simple framework, q *(t ) would have to satisfy (4) U’[q *(t )]/ U’[1- q *(t )] = p2(t )/p (t )}.
6) See, for instance, Buchanan (1967), Ch. 14 and 19, and Buchanan and Tullock (1962), Ch. 13.
7) For simplicity, we are assuming that the decision-making costs depend only on t and not on q .
References
Barbosa, A.S.P. (1978 ), The Constitutional Approach to the Fiscal Process, unp. doctoral dissertation, VPI & SU.
Buchanan, J. and Tullock, G. (1962), The Calculus of Consent, TheUniversity of Michigan Press.
Buchanan, J. (1967) Public Finance in Democratic Process, The University of North Carolina Press, Chapel Hill.
Lerner, A.P. (1944) The Economics of Control, The Macmillan Company, New York.
Rawls, J. (1971) A Theory of Justice, Harvard University Press.
Samuelson, P. (1964) "Lerner at Sixty", Review of Economic Studies, June.