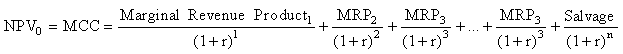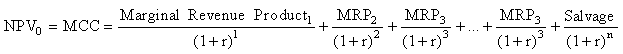
August, 1999

Government Intertemporal Capital Management Decision Making
by David I. Meiselman¹

I have spent some part of my professional career studying private sector capital and capital theory. Part of the motivation for the analysis that follows is to examine whether private sector capital analysis also has relevance to understanding public sector capital management decisions. For the private sector, although there are some unavoidable differences among economists about their judgements of relevant price, income and other elasticities, there is a high degree of consensus on the general nature of saving, investment and capital accumulation and maintenance functions that are central features of the traditional body of economic theory. This also includes the critical role of the rate of interest, the price of time, that permits discounting, capitalization, and intertemporal evaluation and choice.

I use elements of standard capital and price theory to examine some aspects of government intertemporal capital management decisions. There are important differences between private and public capital choices. We later make several assumptions to help focus on some of them. The analysis in this paper differs from the standard cost-benefit analysis or standard project evaluation of specific government proposals or activities. Cost-benefit and project evaluation analyses are typically normative, not positive. They try to answer the go, no go questions, or to rank alternative investment programs, not the positive question how governments do behave. Accordingly, we do not explicitly consider traditional cost-benefit analysis in this paper.

More than realized by the original contributors to the Socialist Calculation discussions of the 1930's, 1940's and earlier (Mises, Lerner, Lange, Hayek, etc.), the absence of a market for used government, capital made impossible a wide range of price discovery and efficiency enhancing choice. For example, if there is no explicit market value for a road or its services and no revenue from its use, how to decide its optimal maintenance for given costs of such repairs. If private repair costs change, there are standard tools to analyze its consequences. (What of changes in public repair costs, say, high pot hole repair costs?) Indeed, there is essentially no theory in the Socialist Calculation debate about what, in fact, governments actually do with respect to capital, because there is essentially little or no useful discussion of public capital management and maintenance. It was as if it was enough to point that the absence of a price system and private property was enough to conclude that governments could not manage capital with the efficiencies inherent in the private sector.

Neither Lerner nor Lange, proponents of thorough, centrally directed Socialism, have any mechanism for government investment in capital or for capital maintenance. Perhaps the deep depression of the 1930's, where capital may have appeared to be in excess of current demands, shifted focus from fundamental questions of how, in fact, governments do or should act.

For present purposes, I wish to avoid the usual Public Choice paradigm that emphasizes the interests of and constraints on politicians, government officials and voters in order to analyze some of the process of government capital decisions. I do so (1) by assuming that governments are ruled by benevolent bureaucrats. I also assume (2) that governments buy capital goods and other inputs in private markets but that governments never sell public capital assets. Government capital assets are essentially inalienable. (I am indebted to James Buchanan who first suggested the assumptions of bureaucratic benevolence and inalienability.) Thus, (3) there is essentially no market for real government capital assets, including used capital.

There are markets for some government liabilities such as tradeable public debts. There are effectively no markets for government assets such as land, aircraft carriers or post office buildings. Because there are no market prices for used government capital assets, there can be no serious calculation that depend on these prices, for example, decisions about optimal maintenance and repair, or buy versus lease decisions. Indeed, one of the surprising implications of this analysis is that governments inherently cannot make efficiency enhancing optimal maintenance and other capital management decisions.

There is another assumption (4) that because capital assets cannot be sold, no gains can be realized on "winners", assets whose market prices have markedly risen. Private owners often have incentives to sell or trade "winners". Governments have no such incentives, here assumed zero. Thus, winners cannot be used to offset losers. Also, (5) we assume no government adjustment to capital losses, either.

Consider briefly some of the standard elements of the analysis of the private market theory of capital and investment. Later, we will consider how the standard analysis generates optimal private maintenance. We continue with the same assumptions regarding government capital decisions (bureaucratic benevolence, no alienation of capital assets and no markets for government capital assets or their services).

Under certainty, the private capital input decision conforms to the usual input optimizing decisions, except that returns (possibly costs, too) are distributed over time. To make measurable values at present and different future times, all future values are discounted to their present values by the use of appropriate interest rates. The result is that the current net marginal cost of a capital good is driven to equality to the present discounted value of the capital good's future stream of net marginal revenue products, each element of which is the product of the capital's marginal physical product and its marginal revenue at alternative optimal outputs. Note also that there is an additional term, Sal, for salvage or scrap value, including resale. In some private decisions, salvage value may be an important consideration in the capital decision. Because of the non-alienability assumption, we also assume no government scrap, salvage or resale values.

In sum, for the certainty case for capital goods at point zero at the beginning of period 1 (now) we have

1. the marginal cost of a capital good (MCC₀)=its net present value₀ (NPV₀).

In turn, the NPV₀ is the discounted sum of the stream of Marginal Revenue Products (MRP) over the life of the capital plus its final or later scrap or salvage value, Sal.

where each MRP value has its net marginal physical product and marginal revenue components included in the MRP calculation. In sum, we have the quantity of capital demanded at current point zero as a function of all of the above variables.

(3) I₀ = I₀ (MCC₀, MPC_1,2,…n, MR_1,2,…m, r, Sal)

Consider some of the implications of the certainty case. First, if there are no salvage or resale values, public and private choice is the same. Second, if there are salvage or resale values but no public sector alienation, public sector present values will be systematically less than private sector ones because scrap values are omitted from the public capital's net future income stream.

One result is that public investment will be sub-optimal and less than optimal private investment. This raises serious questions regarding the oft-repeated assertion that government funded or subsidized investment is required to offset the inherent (and biased) myopia of private market decisions. Under inalienability, gains cannot effectively offset losses; indeed, there are no realized surplus positive values for gains, but there are realized losses from project deficits or losses.

Note also that some of the implications of the inalienability assumption also indicate other sources of inefficiencies of government capital management, especially since the decisions to adjust capital stocks by sales and purchases and by direct investment are crucially altered. The same is true for decisions regarding technology creation and its use, pricing and transfer. These will be discussed in more detail below. Because government can neither price technology efficiently nor rationally control risks by seeking to offset gains and losses, it further calls into question assertions about the supposed inherent technology creating or risk management advantages of the public sector.

Consider instead, the general uncertainty case. Each future variable has a standard subjective mean and also a subjective measure of its dispersion, say, its standard deviation or variance. If there is risk aversion, variance is a "bad", or cost. Alternatively, certain equivalents can be adjusted to account for variance. If there is no "risk aversion" or "risk preference", the mean values are the certainty equivalents.

To isolate the differences between private and public choice, initially assume that both public and private choice are risk neutral and that decisions are made solely on the basis of mathematical (mean) expected (future) values as well as non-alienability. There are systematic differences between private and public choice. These derive from the fact that government decisions and actions are biased because of constraints on selling winning assets. The result is effectively a regime of "heads you don't win, tails you lose". Governments cannot gain from selling capital assets when returns and asset values rise and opportunity costs increase. When values fall, governments and their taxpayers lose. This casts doubt on the ability of a government to make rational, efficiency enhancing sell-buy, rent- lease or similar capital management decisions, particularly long- period horizon choices. It also questions the ability of governments to shift capital intensities in the face of technological change, a change in relative prices of capital inputs, or when other market economic forces alter incentives for factor and product substitutability.

The overall result is that expected public costs are systematically higher than mathematical expectations, including private sector expectations. This analytical result is similar to having greater risk aversion in private choice.

These mechanisms indicate that government regimes end up with the following:

1. higher subjective capital costs,
2. less than optimal capital intensity,
3. less flexibility and slower than optimal adjustment in responding to changes in relative costs and prices,
4. biases that increase as uncertainty increases; with more uncertainty, governments shift to "safer" (excessively safe) solutions,
5. corresponding biases against R.& D. and technological innovation, especially where specific returns are highly uncertain (Note: innovations and R. & D. are complementary with the ability to dispose of obsolescent equipment, so inalienablility leads to less than optimal public technological progress and capital formation),
6. a similar biases against realizing obsolescence, realizing or cutting losses, and moving on,
7. changes in capital asset costs and values are less likely to be reflected in government product prices and factor markets than in private ones,
8. government markets may clear, but solutions are suboptimal.

Consider some related capital market considerations in evaluating the roles of capital and financial markets in analyzing government capital using enterprises. First, there is no government equity market, and equity market information or incentives simply do not exist. There is no effective way high or low growth expectations can be effectively translated to information and incentives for government officials or private investors.

There are extensive markets in government debts, but these are not typically linked to specific enterprises or activities Most federal issues and state and local debts are general obligation bonds, so virtually none of them is linked to the fortunes of individual projects. Thus, the usual private sector interactions with capital and financial markets are missing. There are limited amounts of state and local revenue bonds which effectively moderate these general relationships to a small degree.

Some of the results of the absence of a direct and sensitive link between financial markets and government capital management decisions are derived from the absence of interaction with and information from financial markets:

1. to value public enterprises,
2. to evaluate enterprise or activity management or to facilitate takeovers, mergers, resizing etc.,
3. to reflect expectations or preferences of capital suppliers,
4. to calculate opportunity costs and optimal capital budgeting requirements in solving the problem of deciding how much of which capital to use,
5. to have market evaluations of obligations liabilities of public enterprises, or their outputs or "profits".

Note also that in a regime of non-alienability there is no effective market for used or inventoried tangible assets. This prevents the possibility of incorporating these used capital prices for efficient management of currently held assets. In turn, this precludes the possibility of calculating opportunity costs, making optimizing owning versus leasing decisions, determining optimal maintenance, and the like that are important elements in optimizing private capital management.

When capital asset values rise sharply, governments simply continue to hold the capital despite the higher opportunity costs and the benefits from sale of the higher value assets. There is a long list of formerly cheap, currently dear, land or other assets still retained by government for low value, low intensity uses. These would range from the vast tracts of western lands held by the federal government, the monetary gold stock at Fort Knox, to the use of the Georgetown waterfront on the Potomac River to store sand and salt, and to devoting most of the old army post at the San Francisco Presidio to an officers club and golf course. In effect, governments may inadvertently use or consume high cost capital because the system can effectively ignore the information and the incentives market prices and private property provide. Under similar circumstances, private firms would tend to reshuffle capital asset holdings, use less or none of the higher value capital or more of the lower value capital assets. Unlike governments, private firms have essentially no fixed, costly, century-old capital ikons.

These considerations are also relevant to optimal capital maintenance decisions of governments. In principle, governments may repair pot holes or dams too frequently, in which case the marginal repair costs are not justified by sufficiently higher benefits to road users or taxpayers. Alternatively, pot holes may be repaired too infrequently, so higher benefits of better roads exceed marginal repair costs. The efficiency goal is essentially the optimal level of maintenance.

To make the analytically appropriate decision requires calculation of the (1) present cost of the capital outlay and the (2) present value of the stream of discounted net future benefits.

The calculation must therefore include future valuation changes of capital assets and of capital service streams. The present value of capital maintenance depends on the same general variables as the investment decision, per se.

For governments, under our analytic assumptions, there are no market prices for future capital asset net marginal revenue products, nor are there markets determining future values of capital goods or their scrap values.

Consider a homey example of the private decision to repair a leaking roof. Consider that the alternatives are to patch the roof shingles or to replace the roof. The present cost of patching is less than the present cost of replacing the roof The problem is that patching will have to be repeated in the future over which time there is some probability of structural damage to the house, impairing its market value. The new roof would avoid those later costs, and its improved appearance would tend to increase the value of the property. All of these elements of future payments streams must be appropriately discounted in order to make the optimal decision whether to patch or to replace the roof.

For governments, some of these elements are missing because there is no effective market for used public capital. Governments essentially do not sell or alienate public capital assets and there is no systematic market in which government goods and services are priced and/or traded.

The result is a biased choice towards less than optimal maintenance, or the same myopia Mises discussed more than seventy-five years ago.

Notes