AN INVISIBLE HAND THEOREM FOR COLLECTIVISTS
Earl A. Thompson
University of California, Los Angeles
PREFACE
Although cloistered away for almost two decades now, out of communication with almost all of my old friends, I find no difficulty in recalling the lively, penetrating, and unique mind of Jim Buchanan. What most distinguished Jim to me was his appreciation for sensible novelty. The Jim I remember was quick to recognize the oppressive power of intellectual tradition and rebelled against it whenever it became clear that the tradition posed a substantial barrier to a rational understanding of the world around us. Along with this basic iconoclasm came an unusual appreciation for seeing old things in a new light. No matter how much an idea grated against his basic instincts, he appreciated an idea if it amounted to a logical and empirically meaningful attack on a traditional belief.
But the old Jim may have completely changed. I'd like to know if he has. If so, he will most likely not appreciate the following paper.
ABSTRACT
The "1st and 2nd Welfare Theorems of Economics" establish a basis for praising the free and narrowly rational decisions of individuals living under an idealized form of private property. This paper proves an analogous pair of theorems for collectivist worlds. An analogous application is to unconditionally praise the free decisions of the members of a non-conflictual team and to condemn any centralized attempt to interfere with these rational individual decisions.
The theorem is then generalized to admit a limited form of conflict, one in which subsequent decisionmakers do not appreciate the consumption decisions of their predecessors. This generalized form is most appropriately applied to intertemporal individual decisionmaking and an explanation of the observed lack of personal consumption commitments in stable informational environments.
The theorem and its generalization also apply to political decisions regarding vital institutions. In particular, the theoretical results predict that a group's objective equilibrium choices of its vital institutions, as well as being theoretically efficient, are made in an honest and nonpartisan fashion.
INTRODUCTION
It is commonly observed that in non-conflictual interactions -- i.e., when all of the individuals in a group share the same basic preference orderings over all of their alternative social states -- individuals openly communicate. The team members behave neither deceptively nor aggressively toward others in the group. Even when the environment prevents some members of the group from making decisions with the same quality of information as others in that group, the former individuals are observed to willingly submit to the suggestions of a more informed coordinator, or informal "team leader."
These empirical regularities suggest that the theoretical outcome of narrowly rational, informed individual decisions in non-conflict interactions are always best for the group. In other words, if informed and non-conflicting individuals sequentially maximize, then they will always reach their commonly-desired optimum. The purpose of Part I of this paper is to prove this result, i.e., an invisible hand theorem for collectivists. Actually, it's a much more simple and robust theorem than the analogous theorem that holds for selfish individuals. For proving the two necessary parts of the selfish-individual theorem requires a whole load of additional, quite unrealistic, assumptions.
Yet the new invisible hand theorem has a similar, but much more extreme, laissez faire implication. In fact, it's anarchic. When you're part of a nonconflictual team, you shouldn't have to take any kind of orders from anyone! (Maybe suggestions, but no orders.) People who try to make and enforce rules for the team members (e.g., certain coaches) are fatuous power mongers or misguided paternalists. Such regulation can only interfere with the team's invisible hand and reduce social welfare. If you prize personal freedom, you should appreciate this theorem.
More specifically, the purpose of Part I of this paper is to prove that, in non-conflictual interactions, narrowly rational individual actions under perfect information (a la von Stackelberg and von Neumann-Morgenstern): (1) always generate a solution, and (2) that solution is always a joint optimum. It would be peculiar if (2), our optimality result, which is the simple converse of Bellman's optimality principle, had not been proved elsewhere. We just haven't been able to find the theorem explicitly stated or proved elsewhere. Regarding (1), the existence result, we do find a way to avoid the indifference conundrums posed by Peleg and Yaari for perfect information games when later decisionmakers are indifferent between various solution points. (While Goldman has proved a fairly general existence result for these environments, the pre-existing literature still leaves us without an algorithm for resolving the Peleg-Yaari indifference conundrums.)
Accepting the assumption of universal rationality, the combined existence and efficiency results can be used to test for the existence of conflict. In particular, if individuals are observed to act deceptively or aggressively toward one another, activities that definitionally subtract from the social total, the payoffs are not "team" payoffs. The theorem can be used, for example, to determine whether or not a single consumer -- viewed as a sequence of distinct decisionmakers -- represents a set of conflicting decisionmakers.
A long chain of economic theorists (Strotz, Pollack, Peleg-Yaari, Hammond, Thaler-Shefrin and several other, no-less-sophisticated, thinkers) have argued that our unconstrained future selves are likely to choose future consumption streams that differ from (or are "inconsistent with") the streams that our current selves would most prefer, and that the resulting conflict, an external diseconomy from future to present selves, leads current selves to make commitments constraining the behavior of future selves. However, the standard empirical examples of consumption-commitments -- viz., joining Christmas clubs, avoiding vice-inducing situations (like Odysseus ordering himself tied to the mast), and hiring budget-enforcing agents -- are not unambiguous examples of such constraints. Rather, a bit of introspection suggests that these are examples of constraints imposed on future selves that are less informed, impulse-buying, selves than the current, more thoughtful, self. The literature's inability to isolate clean examples of such consumptive "time inconsistencies" speaks for a genuine empirical rarity of intrapersonal consumption externalities from informed future selves to informed present selves.
We can thus take the absence of consumption commitments in situations where the individuals are continually well-informed to imply an absence of consumption externalities from future selves to current selves. A person's informed future consumption choices do not displease the person's informed current self. But an absence of commitments does not imply a complete absence of conflict. Current selves may still impose externalities on, or do things that displease, their future selves. Part II of this appendix correspondingly shows that, under perfect information, a no-commitment solution under this limited form of conflict remains optimal for the externality-imposing current decisionmaker. Viewing the current individual as the appropriate social target, the theorem -- which generalizes a consistency theorem of Blackorby, Nissen, Primont, and Russell -- is a generalization of our theorem to worlds with exclusively forward-looking, or "ungrateful", future decisionmakers.
A generalization of these theorems allowing them to apply to certain political interactions is discussed in Part III.
I. THE CENTRAL THEOREM
A convenient description of the first non-conflict situation has the utilities of each of the individuals in a group represented by monotone increasing functions of a common, continuous, real-valued function of individual actions, f(x1,...,xn), where the action, xi, of the ith individual, i = 1,...,n, is chosen from a compact set of feasible actions, Xi.
If the individuals in this situation independently (or simultaneously) chose their actions, each selecting an xi that maximized f for given (x1,...,xi-1,xi+1,...,xn), the resulting, Cournot-type, solution set might obviously contain many local maxima that are not global maxima. There would be nothing to guarantee the achievement of a globally maximal value of f. The source of the problem is that the decisionmakers have no information about one another's actions, and therefore there is no genuine "coordination" of their activities.
To represent genuinely "coordinated," noncooperative decisionmaking, we assume "perfect information" in the von Stackelberg-von Neumann-Morgenstern sense, meaning that the individuals choose their actions in sequence, where individual 1 chooses first and then, in full knowledge of this move, individual 2 chooses an action. This continues on until the nth individual chooses an action xn in Xn that maximizes f(x1,...,xn-1,xn) for the known, previously chosen, values of x1,...,xn-1. We first show that a pure-strategy solution to the above game always exists.
The existence of an optimal xn for the last mover is assured by the compactness of Xn and the continuity of f (for a proof, see Apostol, p. 73). There may be several such maximizing values of xn. We shall let x(x1,...,xn-1) represent n's solution correspondence. Since x is going to be so picked, individual n-1 will attempt to pick an xn-1 that maximizes, for given x1,...,xn-2, the function f(x1,...,xn-2,
xn-1,x(x1,...,xn-2,xn-1)). Since the value of f for a given xn-1 is the same regardless of the value of xn subsequently chosen from the non-empty image set of x(x1,...,xn-1), the actual choice by n from this set is a matter of indifference to n-1 as well as to n and therefore does not affect the choice by n-1. Momentarily assuming the existence of a maximizing solution for individual n-1, an assumption validated in the next paragraph, the maximization yields another non-empty correspondence, x-1(x1,...,xn-2). Similarly, individual n-2 attempts to pick, prior to the choice of n-1 and n, an xn-2 that maximizes, for given x1,...,xn-3, f(x1,...,xn-3,xn-2,x-1(x1,...,xn-3,xn-2,x(x1,...,xn-3,
xn-2,x-1(x1,...,xn-3,xn-2))). A solution set to this sequence of n maximizations, (x*), may, of course, contain several elements.
To prove that the set is non-empty, it is sufficient to prove that the above-described response correspondences, x-1( ),...,x( ), are all non-empty. Again, x-1( ) is non-empty if the domain of the objective function variables controlled by n-1 (i.e.,
(xn-1,x(xn-1))) is compact (Apostol, ibid). Since the domain of xn-1,Xn-1, is compact by assumption, we need only show that the range of x(xn-1), or 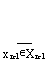 x(xn-1), is compact. This is done in the following three steps: First, because (xn-1,x(xn-1)) maximizes a continuous, real-valued objective function for a given xn-1, we know that x(xn-1) is upper-semicontinuous (Berge). Second, x(xn-1) is closed for any given value of xn-1. For suppose otherwise; then the set x(xn-1) would not contain all of its limit points. Call one of these excluded limit points z. Since Xn is closed, z 0 Xn. And since z is not in x(xn-1), f(x1,...,xn-1,z) < f(x1,...,xn-1, x(xn-1)). From these facts, it would follow that
x(xn-1), is compact. This is done in the following three steps: First, because (xn-1,x(xn-1)) maximizes a continuous, real-valued objective function for a given xn-1, we know that x(xn-1) is upper-semicontinuous (Berge). Second, x(xn-1) is closed for any given value of xn-1. For suppose otherwise; then the set x(xn-1) would not contain all of its limit points. Call one of these excluded limit points z. Since Xn is closed, z 0 Xn. And since z is not in x(xn-1), f(x1,...,xn-1,z) < f(x1,...,xn-1, x(xn-1)). From these facts, it would follow that 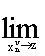 f(x1,...,xn-1,x(xn-1)) > f(x1,...,xn-1,z), which contradicts the continuity of f. So x(xn-1) is an upper-semicontinuous function with a closed image for any given xn-1. We can now complete the proof by applying the result of Nikaido (Lemma 4.5) stating that such a function defined over a compact set produces a total image set, our
f(x1,...,xn-1,x(xn-1)) > f(x1,...,xn-1,z), which contradicts the continuity of f. So x(xn-1) is an upper-semicontinuous function with a closed image for any given xn-1. We can now complete the proof by applying the result of Nikaido (Lemma 4.5) stating that such a function defined over a compact set produces a total image set, our 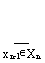 x(xn-1), which is compact. So x-1(x1,...,xn-2) is non-empty. The same procedure can be repeated to show that x-2(x1,...,xn-2) is non-empty, etc.
x(xn-1), which is compact. So x-1(x1,...,xn-2) is non-empty. The same procedure can be repeated to show that x-2(x1,...,xn-2) is non-empty, etc.
This completes our existence proof. We are now prepared to discuss optimality.
In general, that is, when conflict may be present, perfect information solutions are not generally jointly efficient. Standard Prisoner's Dilemma games illustrate this simple fact. But we are dealing here with a non-conflict situation, where the possible payoffs do not permit the redistributional opportunities presented in a standard Prisoner's Dilemma game.1
We now prove that a perfect information solution will always achieve a joint optimum in the above, non-conflict situation:
Suppose that a member of the solution set, say x*, were not a global maximum point. Then there would be an alternative xo 0 X =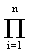 Xi, such that f(xo) > f(x*). Had individual n been presented with x, ...,x-1, the individual would have picked x (i.e., x(x,...,x-1) = x); and xo would have resulted instead of x*. It follows that n was not presented with (x,...,x-1). It similarly follows that if individual n-1 had been presented with x,...,x-2, the individual would have picked x-1; for x(x,...,x-1) = x and f(xo) > f(x*). So n-1 was not presented with x,...,x-2. For the same reason, individual n-2 was not presented with x,...,x-3, etc., up to individual 1. But individual 1 has no excuse. Individual 1 must have not maximized utility. For, according to the above sequence, wherein x* … x0 implies x … x, if individual 1 had picked x = x, then the outcome would have equalled xo and individual 1's utility would have been higher. So the supposition that x* is not a global maximum contradicts the assumption of individually rational choice. The solution point x* must be a global maximum.
Xi, such that f(xo) > f(x*). Had individual n been presented with x, ...,x-1, the individual would have picked x (i.e., x(x,...,x-1) = x); and xo would have resulted instead of x*. It follows that n was not presented with (x,...,x-1). It similarly follows that if individual n-1 had been presented with x,...,x-2, the individual would have picked x-1; for x(x,...,x-1) = x and f(xo) > f(x*). So n-1 was not presented with x,...,x-2. For the same reason, individual n-2 was not presented with x,...,x-3, etc., up to individual 1. But individual 1 has no excuse. Individual 1 must have not maximized utility. For, according to the above sequence, wherein x* … x0 implies x … x, if individual 1 had picked x = x, then the outcome would have equalled xo and individual 1's utility would have been higher. So the supposition that x* is not a global maximum contradicts the assumption of individually rational choice. The solution point x* must be a global maximum.
Jim Mirrlees has privately suggested an alternative, more direct, optimality proof. It can be paraphrased as follows: Pick any x. Then change xn so that it maximizes f for the given x1,...,xn-1. The resulting f defines a particular value of a function,
fn-1[x1,...,xn-1]. Then pick an xn-1 that maximizes the latter function, thus yielding an f that defines fn-2[x1,...,xn-2], etc. By definition, f1 $ f2[x1] $ ... $ fn-1[x1,...,xn-1] $ f[x1,...,xn]. Since f1 depends on no variables, it is, according to Mirrlees, unique and therefore the same regardless of what value of x we initially chose. In particular, if x = x0, f1 = f2 = ... = fn-1 = f(x0) =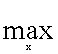 f(x1,...,xn). So f1 is our maximum and the theorem is proved.
f(x1,...,xn). So f1 is our maximum and the theorem is proved.
Maxim Engers has pointed out that the optimality theorem leads to a simple alternative, albeit less direct, existence proof: Since the converse of this optimality theorem, Bellman's Optimality Principle, also holds, a sequential maximization solution is equivalent to a maximum. Therefore, since a maximum in our model exists, so does a sequential maximization solution. Unfortunately, this existence proof does not extend to the generalized problem of Section II while our more cumbersome, direct, proof does.
II. A GENERALIZATION ALLOWING FOR
UNGRATEFUL FUTURE DECISIONMAKERS
As noted in the Introduction, the absence of incentives to devote resources gaining transfers from others implied in the above non-conflict situation continues to hold under a weakening of the conditions on preferences. In particular, it continues to hold as long as each future decisionmaker has the same preferences over future actions as the immediately preceding decisionmaker. In this case, the successive objective functions are:
f1(x) = U1(x1,f2(x))
f2(x) = U2(x1,x2,f3(x))
.
.
fn-1(x) = Un-1(x1,...,xn-2,xn-1,fn(x))
fn(x) = Un(x1,...,xn-1,xn),
where f +1 > f+1 6 Ui(x1,...,xi,f+1) > Ui(x1,...,xi,f+1). Thus, for any given x1,..., xi, the ith individual's objective function is a monotone increasing function of the i + 1st individual's function.
A particular perfect information solution, xr, is, as above, an x such that: x is picked so as to maximize fn(x); x-1 is picked so as to maximize fn-1(x) given x1,...,xn-2 and the dependence of x or xn-1, etc. The existence of a solution holds under the same conditions on preferences, and through the same argument, as in the direct proof of Section I; the exercise will not be repeated.
What we wish to show is that no decisionmaker has an incentive to influence later decisionmakers, i.e., that all subsequent decisionmakers will choose a sequence of actions that maximizes the utility of a current decisionmaker. From this it follows that a current decisionmaker has no incentive to threaten to punish, or withhold information from, future decisionmakers.
The result holds trivially for i = n. To show it for i = n-1, first note that our above specification on the forms of the successive objective functions implies that any xn that maximizes fn given x1,...,xn-1 will also maximize fn-1 given x1,...,xn-1. Therefore, n will choose the xn that maximizes the utility of n-1, say n's mother, as long as any pair of actions resulting from n-1's first rationally picking an xn-1 in anticipation of her own subsequent utility-maximizing choice of an xn -- call the pair x-1,x -- unconditionally maximizes her utility, fn-1(x,...,x-2,xn-1,xn) over all xn-1,xn in Xn-1 H Xn. Theorem 1 -- that rational, perfectly informed, sequential choice under a common utility function achieves an unconditional maximum of that function, tells us that x-1,x does indeed unconditionally maximize fn-1(x,...,x-2,xn-1,xn). Building on this, we can show in the same way that x-2,x-1,x unconditionally maximizes fn-2(x,...,x-3,xn-2,
xn-1,xn), and so on until we arrive at individual 1, at which point our theorem is proved.
III. SUPPLYING VITAL INSTITUTIONS
In ordinary, selfish, human societies, the basic object of rational choice, as emphasized in Thompson-Faith, is the reaction function. What we have been calling "rational", or "narrowly rational", choice would then apply to a choice among alternative reaction functions.
In particular, once the rent-determining reaction functions that define the society are established, the joint-survival-determining reaction-functional choices necessary for the defense of these societies are not the subject of internal conflictual interaction. Thus, once the initial distributional issues are settled, there should be no disagreement among equally informed individuals on the existence, for example, of a continued armed response to an attack, its method of finance, an intermediate military hierarchy, etc. Abstracting again from honest disagreements, the political and military decisions that set up such non-controversial institutions should therefore possess the same lack of deception and inter-personal aggressiveness -- the same lack of rent-seeking when interpreting these activities in a social context -- that exists in the above model.
In other words, equilibrium social decisions as regards various vital institutions, besides being efficient, are made in an honest and non-partisan fashion. Moreover, applying our generalized theorem (Section II above), the vital military obligations that current political decisionmakers impose on their future selves must be similarly regarded as efficient obligations despite the possible disagreement of the future decisionmakers.
Unlike the other applications, some commitments are essential. If the announced responses to foreign aggression are not substantially carried out, if the announcements are hollow threats, the shared social surplus will be lost. Nevertheless, an individual may easily feel better-off as a probably-live coward than a probably-dead hero; and even the whole society may easily feel "better red than dead" or that war debts are negotiable. Aggression against cowards, and conflict at the onset of a war or over the payment of war debts, are thus inevitable. The non-conflictual interaction, and hence the theory of this section, must therefore be carefully restricted to the strictly pre-war setting in which defense institutions are being established.
Hence, the test should come during peacetime, especially during military preparation. One such test is the absence of ordinary rent-seeking, or "partisan", politics in choosing to adopt a set of collectively vital defense institutions.
A FINAL SUGGESTION
For almost two centuries now, our universities have featured an artificial economic debate between individuals extolling the virtues of free markets and those extolling the virtues of utopian socialism. Even a cursory reading of the influential authors -- including Professor Buchanan -- informs us that the former are actually extolling the virtues of free markets only where people are not significantly benevolent (e.g., in Adam Smith's butcher shop) and that the latter [utopians are not Marxists] are extolling the virtues of anarchic socialism only where people are highly benevolent toward one another (e.g., in a Christian monastery).
These entertaining debaters should drop the pretense and merge. Both, now, have an invisible hand theorem to support their policy positions. There is as much logic to support one position as there is to support the other. There are areas of an economy in which pure benevolence (where individuals share the same payoff function) is a useful assumption and other areas where benevolence can be totally ignored. And neither school has much to say about models containing intermediate levels of benevolence. There is just no obvious reason for these two schools to disagree with one another.
More importantly, the two schools of thought (now that both are theoretically supported) share a common policy implication. Suppose, as members of both schools appear to believe that the elites of almost any society use their influence over education to grab a substantial and unjustified amount of administrative authority over others. The two schools' respective invisible hand theorems then tell us that otherwise efficiently structured societies will be observed to suffer from: (1) the regulation of competitive markets that are devoid of externalities, and (2) the enforcement of rules against specific members of teams that possess no internal conflict. The two forms of evidence are quite complementary. And if evidence regarding one implication is prohibitively costly to produce, evidence supporting the other implication would lend substantial credence to their shared social hypothesis.
NOTES
1
An additional, well-known difficulty with perfect information solutions is that when a later mover is indifferent between several possible actions, prior movers -- not knowing which among the later mover's indifferent actions will actually be selected -- do not really know what to do. This difficulty also disappears in non-conflict situations because, as we have already indicated, when prior movers always share the indifference of later ones, the particular actions of later movers within their solution correspondences have no effect on the utilities or decisions of prior movers.
REFERENCES
Apostol, T.M., Mathematical Analysis, Reading MA: Addison Wesley, 1957.
Berge, C., Topological Spaces, Including a Treatment of Multi-valued Functions, Vector Spaces and Convexity, Edinburgh: Oliver and Boyd, 1963.
Blackorby, C., D. Nissen, D. Primont, and R.R. Russell, "Consistent Intertemporal Decision Making," Review of Economic Studies, Apr. 1972: 239-48.
Buchanan, James M., Freedom in Constitutional Conact: Perspectives of a Political Economist, College Station, TX and London: Texas A&M University Press, 1977, pp. 4-5.
Goldman, S.M., "Consistent Plans," Review of Economic Studies, 148, Apr. 1980: 533-39.
Hammond, P.J., "Changing Tastes and Coherent Dynamic Choice," Review of Economic Studies, 133, Feb. 1976: 159-73.
Nikaido, H., Convex Structure and Economic Theory, New York: Academic Press, 1968.
Peleg, B., and M.E. Yaari, "On the Existence of a Consistent Course of Action When Tastes are Changing," Review of Economic Studies, July 1973: 391-402.
Pollak, R.A., "Consistent Planning," Review of Economic Studies, 102, Apr. 1968: 202-08.
Strotz, R.H., "Myopia and Inconsistency Under Dynamic Utility Maximization," Review of Economic Studies, 23, 1956: 165-80.
Thaler, R.H., and H.M. Shefron, "An Economic Theory of Self Control," Journal of Political Economy, 89, Apr. 1981: 392-406.
Thompson, E.A., and R.L. Faith, "A Pure Theory of Strategic Behavior and Social Institutions," American Economic Review, 71, June 1981: 366-81.
von Neumann, J., and O. Morgenstern, Theory of Games and Economic Behavior, 3rd ed., Princeton: Princeton University Press, 1953.
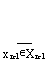 x(xn-1), is compact. This is done in the following three steps: First, because (xn-1,x(xn-1)) maximizes a continuous, real-valued objective function for a given xn-1, we know that x(xn-1) is upper-semicontinuous (Berge). Second, x(xn-1) is closed for any given value of xn-1. For suppose otherwise; then the set x(xn-1) would not contain all of its limit points. Call one of these excluded limit points z. Since Xn is closed, z 0 Xn. And since z is not in x(xn-1), f(x1,...,xn-1,z) < f(x1,...,xn-1, x(xn-1)). From these facts, it would follow that
x(xn-1), is compact. This is done in the following three steps: First, because (xn-1,x(xn-1)) maximizes a continuous, real-valued objective function for a given xn-1, we know that x(xn-1) is upper-semicontinuous (Berge). Second, x(xn-1) is closed for any given value of xn-1. For suppose otherwise; then the set x(xn-1) would not contain all of its limit points. Call one of these excluded limit points z. Since Xn is closed, z 0 Xn. And since z is not in x(xn-1), f(x1,...,xn-1,z) < f(x1,...,xn-1, x(xn-1)). From these facts, it would follow that 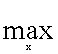 f(x1,...,xn). So f1 is our maximum and the theorem is proved.
f(x1,...,xn). So f1 is our maximum and the theorem is proved.